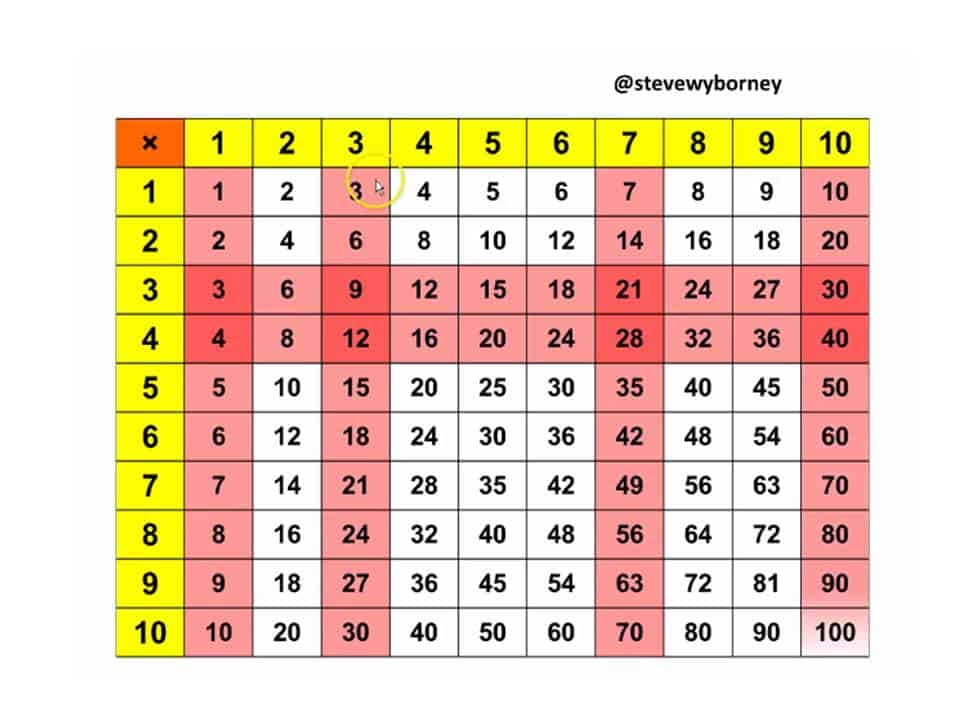
I made multiplication table using PowerPoint and went on to discover some very interesting relationships within the table.
You will see several here. Watch the video below.
Click here to download the animated Multiplication Table.
(After downloading, your first step will be to click the multiplication symbol to clear the table.)
Click here to download the animated Multiplication Table.
Other posts that may interest you:
- The Maze Hundreds Chart
- Tiled Area Questions
- Introducing Cube Connectors
- Color the Cube Connectors
- Experiencing Subitizing
- Provide Massive Space to Notice
You may also be interested in viewing and downloading The Green Light Hundreds Chart.
See the updated video: Is This Claim Always True? A powerful post to use in your classroom.

Leave a Reply